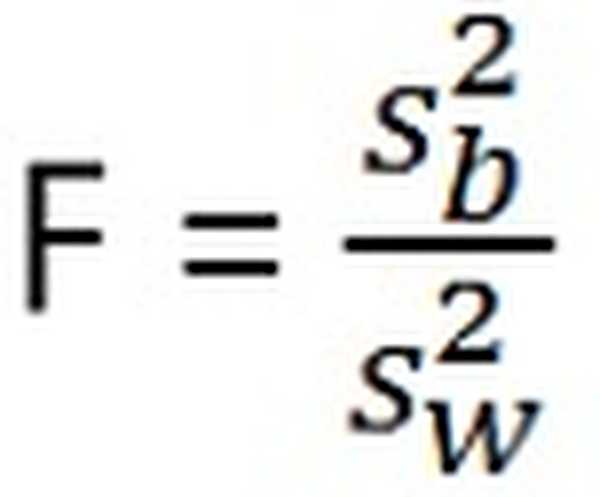Разница между Т-тестом и ANOVA
 Share
Share
 Существует тонкая линия демаркации между t-тестом и ANOVA, то есть, когда необходимо сравнить средние значения только двух групп, Т-тест используется, но при сравнении средств более двух групп, ANOVA является предпочтительным.
Существует тонкая линия демаркации между t-тестом и ANOVA, то есть, когда необходимо сравнить средние значения только двух групп, Т-тест используется, но при сравнении средств более двух групп, ANOVA является предпочтительным.
T-тест и дисперсионный анализ, сокращенно обозначенные как ANOVA, представляют собой два параметрических статистических метода, используемых для проверки гипотезы. Поскольку они основаны на общепринятом предположении, например, что население, из которого отбирается выборка, должно быть нормально распределено, дисперсия однородности, случайная выборка данных, независимость наблюдений, измерение зависимой переменной на уровне отношения или интервала, люди часто неправильно их интерпретируют. два.
Вот статья, представленная для вас, чтобы понять существенную разницу между t-тестом и ANOVA, посмотрите.
Содержание: T-тест против ANOVA
- Сравнительная таблица
- Определение
- Ключевые отличия
- Вывод
Сравнительная таблица
| Основа для сравнения | Т-тест | ANOVA |
|---|---|---|
| Смысл | T-критерий - это критерий гипотезы, который используется для сравнения средних значений двух групп населения.. | ANOVA - это статистический метод, который используется для сравнения средних значений для более чем двух групп населения.. |
| Тестовая статистика | (x ̄-µ) / (s / √n) | Между выборочной дисперсией / внутри выборочной дисперсии |
Определение Т-теста
T-критерий описывается как статистический критерий, который проверяет, сильно ли отличаются значения совокупности двух выборок, используя t-распределение, которое используется, когда стандартное отклонение неизвестно, а размер выборки невелик. Это инструмент для анализа, взяты ли две выборки из одной популяции.
Тест основан на t-статистике, которая предполагает, что переменная обычно распределена (симметричное колоколообразное распределение), а среднее известно и дисперсия населения рассчитывается по выборке..
В t-тесте нулевая гипотеза принимает форму H0: µ (x) = µ (y) против альтернативной гипотезы H1: µ (x) ≠ µ (y), где µ (x) и µ (y) представляют собой совокупность. Степень свободы t-теста1 + N2 - 2
Определение ANOVA
Дисперсионный анализ (ANOVA) является статистическим методом, обычно используемым во всех тех ситуациях, когда необходимо проводить сравнение между более чем двумя популяционными средствами, такими как урожайность из нескольких сортов семян. Это жизненно важный инструмент анализа для исследователя, который позволяет ему проводить тестирование одновременно. Когда мы используем ANOVA, предполагается, что выборка взята из нормально распределенной популяции, а дисперсия популяции равна.
В ANOVA общее количество изменений в наборе данных делится на два типа, то есть количество, назначенное случайности, и количество, назначенное определенным причинам. Его основной принцип заключается в проверке различий между средствами населения путем оценки количества различий внутри групповых предметов, пропорционального количеству различий между группами. В пределах выборки разница обусловлена случайным необъяснимым нарушением, тогда как различная обработка может привести к дисперсии выборки..
С помощью этой техники мы проверяем нулевую гипотезу (H0) где все популяции означают одинаковые или альтернативные гипотезы (H1) где по меньшей мере одно среднее значение отличается.
Ключевые различия между T-test и ANOVA
Существенные различия между T-тестом и ANOVA подробно обсуждаются в следующих пунктах:
- Тест гипотезы, который используется для сравнения средних значений двух групп населения, называется t-тестом. Статистический метод, который используется для сравнения средних значений для более чем двух групп населения, известен как Анализ отклонений или ANOVA..
- Статистика теста для T-теста:
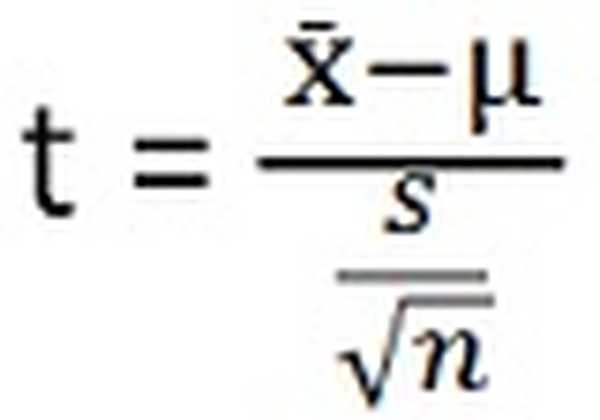 Тестовая статистика для ANOVA:
Тестовая статистика для ANOVA: 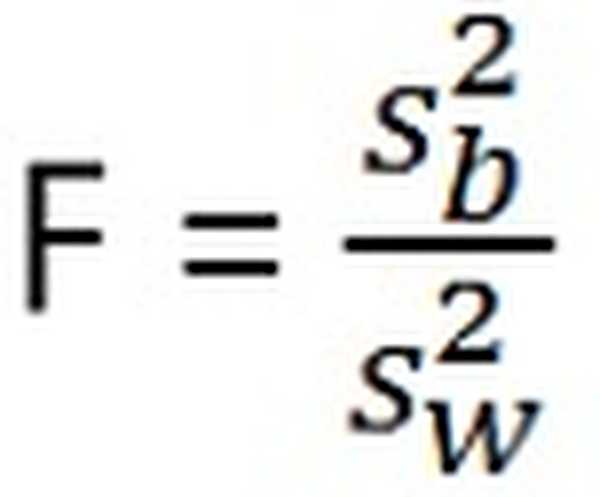
Вывод
Изучив вышеприведенные пункты, можно сказать, что t-тест - это особый тип ANOVA, который можно использовать, когда у нас есть только две популяции для сравнения их средних значений. Хотя вероятность ошибок может возрасти, если использовать t-критерий, когда мы должны сравнивать более двух средних по совокупности, именно поэтому используется ANOVA
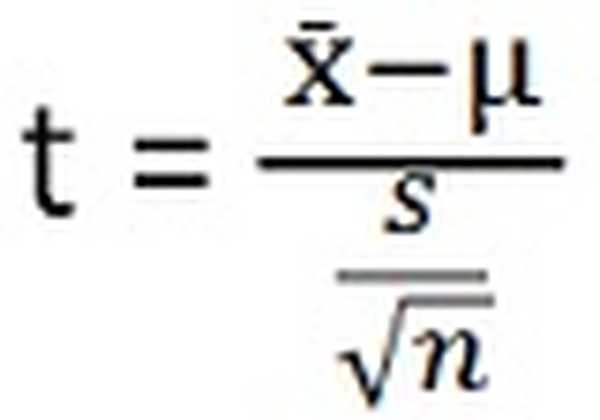 Тестовая статистика для ANOVA:
Тестовая статистика для ANOVA: